This post is the presented script of the lecture given on 2020-09-11, which introduces the basics of support-vector machines and its practice.

本文为 2020-09-11 所做讲座的文稿，介绍了支持向量机的基础知识与应用实践。

1 Basics / 基础知识

1.1 Concepts / 基本概念

In machine learning, support-vector machines are supervised learning models with associated learning algorithms that analyse data used for classification and regression analysis.
The support-vector clustering algorithm is used to categorize unlabelled data.
Clustering is unsupervised learning.

A linear classifier (线性分类器) separates $p$-dimensional vectors (data points) with a $(p-1)$-dimensional hyperplane.
A hyperplane (超平面) is a subspace whose dimension is one less than of its ambient space. If a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines.
An ambient space (环绕空间) is the space surrounding a mathematical object, along with the object itself. For example, a 1-dimensional line ($l$) may be studied in isolation, in which case the ambient space of $l$ is $l$; or it may be studied as an object embedded in 2-dimensional Euclidean space ($\mathbb{R}^{2}$), in which case the ambient space of $l$ is $\mathbb{R}^{2}$; or as an object embedded in 2-dimensional hyperbolic space ($\mathbb{H}^{2}$), in which case the ambient space of $l$ is $\mathbb{H}^{2}$. Consider the statement “parallel lines never intersect”, this is true if the ambient space is $\mathbb{R}^{2}$, but false if the ambient space is $\mathbb{H}^{2}$.

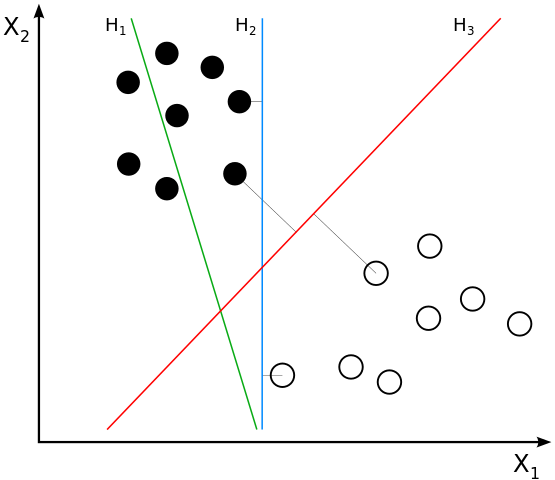
The margin of a single data point is defined to be the distance from the data point to a decision boundary (决策边界). One reasonable choice as the best hyperplane is the one that represents the largest margin between two classes.

More formally, a support-vector machine constructs a hyperplane or set of hyperplanes in a high-dimensional space, which can be used for classification, regression, or other tasks like outlier detection. Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training data point of any class, since in general the larger the margin, the lower the generalization error of the classifier.

A support-vector machine is a maximum-margin hyperplane classifier.

1.2 Linear SVM / 线性支持向量机

Hard-margin: If the training data is linearly separable, we can select two parallel hyperplanes that separate the two classes of data, so that the distance between them is as large as possible. The region bounded by these two hyperplanes is called the “margin”, and the maximum-margin hyperplane is the one that lies halfway between them.
Note that the maximum-margin hyperplane is completely determined by the data points (vectors) on the two parallel hyperplanes. These vectors are called support vectors.

Soft-margin: If the training data is not linearly separable, introduce hinge loss function.

1.3 Nonlinear classifier / 非线性分类器

Whereas the original problem may be stated in a finite-dimensional space, it often happens that the sets to discriminate are not linearly separable in that space. For this reason, it was proposed that the original finite-dimensional space be mapped into a much higher-dimensional space, presumably making the separation easier in that space.

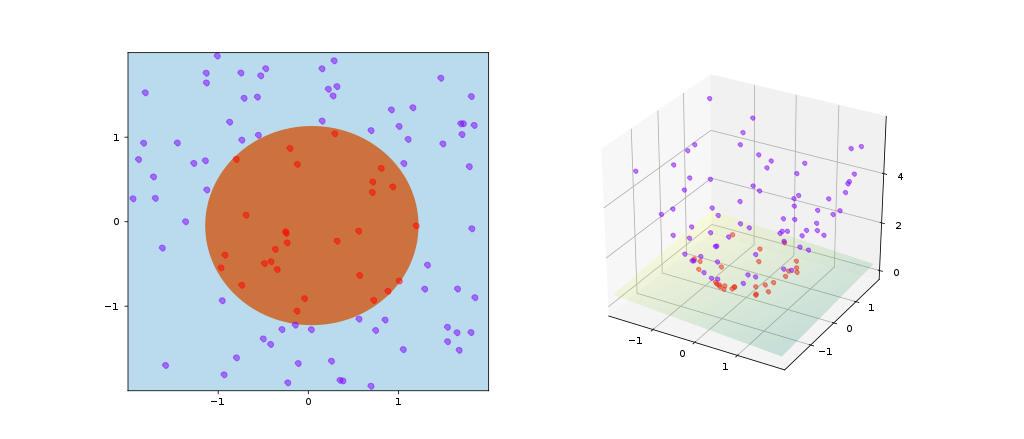
Some common kernels:

• Linear: $k(\vec{x_i}, \vec{x_j})=x_i^T x_j$
• Polynomial (homogeneous): $k(\vec{x_i}, \vec{x_j})=(\vec{x_i} \cdot \vec{x_j})^d$
• Polynomial (inhomogeneous)
• Gaussian radial basis function (RBF): $k(\vec{x_i}, \vec{x_j})=\exp(-\gamma |\vec{x_i}-\vec{x_j}|^2)$ for $\gamma >0$, sometimes parametrized using $\gamma =1/(2\sigma^2)$.
• Hyperbolic tangent

1.4 Parameter selection / 参数的选择

The effectiveness of SVM depends on the selection of kernel, the kernel’s parameters, and soft margin parameter $C$. A common choice is a Gaussian kernel (RBF kernel), which has a single parameter $\gamma$. The best combination of $C$ and $\gamma$ is often selected by a grid search with exponentially growing sequences of $C$ and $\gamma$, for example, $C \in {2^{-5}, 2^{-3}, \ldots, 2^{13}, 2^{15}}$; $\gamma \in {2^{-15}, 2^{-13}, \ldots, 2^{1}, 2^{3}}$. Typically, each combination of parameter choices is checked using cross validation, and the parameters with the best cross-validation accuracy are picked.

Parameters illustrated: SVC Parameters When Using RBF Kernel (scikit-learn)

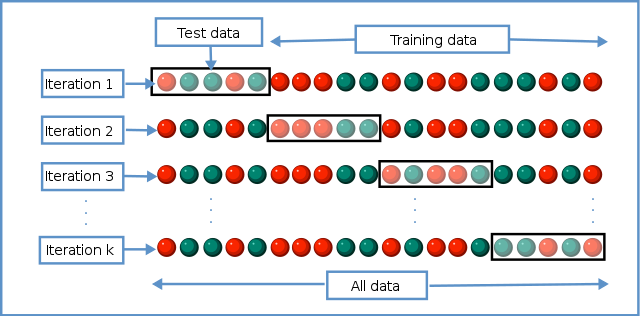
The goal of cross-validation is to test the model’s ability to predict new data that was not used in estimating it, in order to flag problems like overfitting or selection bias.
One round of cross-validation involves partitioning a sample of data into complementary subsets, performing the analysis on one subset (training set), and validating the analysis on the other subset (validation set or testing set).

1.5 Extensions / 扩展概念

Support-vector clustering (SVC)
Multiclass SVM
Support-vector regression (SVR)

2 Practice / 应用实践

2.1 Data pre-processing / 数据预处理

Categorical attributes should be converted into numeric data. It is recommended to use m numbers to represent an m-category attribute. For example, a three-category attribute {red, green, blue} can be represented as (0,0,1), (0,1,0), and (1,0,0). Experiences indicate that if the number of values in an attribute is not too large, this coding might be more stable than using a single number.

Scaling before applying SVM. The main advantage of scaling is to avoid attributes in greater numeric ranges dominating those in smaller numeric ranges. Another advantage is to avoid numerical difficulties during the calculation. Because kernel values usually depend on the inner products of feature vectors, large attribute values might cause numerical problems. It is recommended to linearly scale each attribute to the range [-1,+1] or [0,1]. Remember to use the same method to scale both training and testing data.

2.2 Model selection / 模型的选择

The RBF kernel is a reasonable first choice. This kernel (1) can handle the case when the relation between class labels and attributes is nonlinear, (2) with certain parameter $(C, \gamma)$ behaves like a linear kernel or a sigmoid kernel, (3) has less hyperparameters than polynomial kernel, (4) has fewer numerical difficulties.

In particular, when the number of features is very large, one may just use the linear kernel.

2.3 Cross-validation / 交叉验证

It is recommended to perform grid-search on $C$ and $\gamma$ using cross-validation. It is found that trying exponentially growing sequence of $C$ and $\gamma$ is a practical method to identify good parameters. Use a coarse grid first to identify a “better” region, then conduct a finer grid search on that region.

2.4 When to use linear but not RBF kernel? / 只需使用线性分类器的场景

• Number of instances ≪ number of features
• Both numbers of instances and features are large
• Number of instances ≫ number of features

3 Libraries / 库

LIBSVM: An integrated software for support vector classification, regression, and distribution estimation (one-class SVM). Sources in C++ and Java, with extensions for many other languages.
License: BSD
Site @ National Taiwan University, with data sets.

LIBLINEAR: A linear classifier for data with millions of instances and features.
License: BSD
Site @ National Taiwan University

libsvm-mat: MATLAB extended toolbox for LIBSVM.
License: Unknown
libsvm-mat-2.89-3 – MATLAB技术论坛
SVM相关资源 – faruto – MATLAB技术论坛

4 Further reading / 延伸阅读

支持向量机通俗导论（理解 SVM 的三层境界）: Post on CSDN with PDF version appended at the end.

CS229 Lecture notes—Part V—Support Vector Machines: PDF file (from Stanford’s Machine Learning Course by Andrew Ng)